이산수학_이산수학 기초

📚 이산 수학 ( Discrete Mathmatics )

이산 수학 개요

• 이산 수학

  • 참과 거짓으로 살펴보는 컴퓨터를 위한 수학
  • 불연속적인 숫자를 다루는 수학
  • 컴퓨터 과학의 베이스 학문
  • 컴퓨팅 사고를 길러준다

명제와 연산자

명제

• 참 or 거짓으로 진리를 정확하게 구분할 수 있는 문장
• 명제는 0 또한 1만 가지는 컴퓨터의 메모리처럼 항상 참과 거짓 둘 중 하나의 값만을 가진다.

• 여러가지 명제를 조합 가능

• 예시
  • 원빈은 잘생겼다 : X ( 명제 X )
  • 컴퓨터는 재미가 없다 : X ( 명제 X )
  • 숫자 11은 소수이다 : O ( 참 )
  • 모기는 동물이다 : O ( 참 )

연산자

• 명제를 연산하기 위한 도구
• 6가지의 기본 연산자
  • ￢ : Not
    • 거짓 : 참일땐 거짓, 거짓일땐 참
  • ∧ : And
    • 논리곱 : 둘 다 참일 때 참
  • ∨ : Or
    • 논리합 : 둘 중에 하나만 참이면 참
  • ⊕ : Exclusive or
    • 배타적 논리합 : 한 개만 참일 때만 참
  • → : Implication
    • 조건 명제 ( 함축 ) : p->q p일때 q이다. 조건과 결과를 나타낸다
    • T -> T : T
    • T -> F : F
    • F -> T : T
    • F -> F : T
  • ↔ : Biconditional
    • 쌍방 조건 명제 : 서로 값이 일치할 때만 참

역, 이, 대우

• 진리표

  • 각 명제 사이의 관계식의 진릿값을 보여주는 표
  • 아무리 복잡한 합성 명제라도 진리표로 풀어낼 수 있다.

• 역, 이, 대우는 조건 명제에서 사용한다. ( p -> q )

역

• p와 q 위치를 바꾸는 것을 역이라 한다.
• q -> p

이

• 각각의 명제에 부정을 붙이는 것
• ￢ p -> ￢ q

대우

• 증명하기 어려운 명제는 대우를 이용해 증명할 수 있다. ( 역, 이 , 대우를 사용하는 이유)
• 역과 이를 합친 것
• ￢ q -> ￢ p

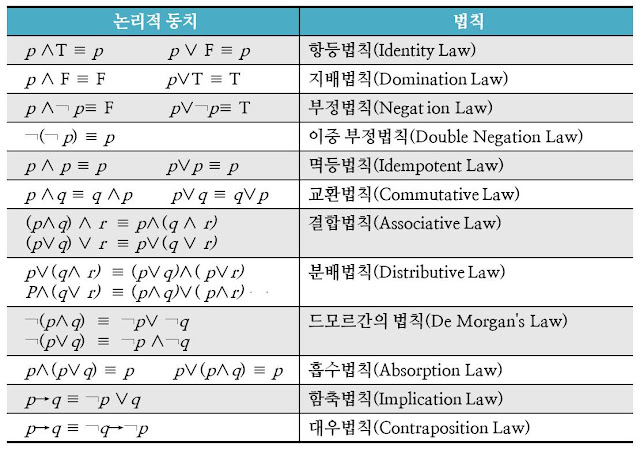
동치

• 동치

  • 논리적으로 일치한다.
  • 동치는 같은 의미를 가진 더 쉬운 명제를 발견하는데 사용한다.
  • 여러 동치법칙이 있다.

• 동치 법칙

  • 드모르간 법칙이 많이 사용된다.