ALGORITHM_위상 정렬 ( Topological sort )
📚 ALGORITHM

📚 위상 정렬 ( Topological sort )
위상 정렬 이란?
어떤 일들에 순서가 정해져 있을 때 순서에 맞게 나열하는 행위이다.
즉, 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것이다.
예시를 통해 이해를 도와보겠다.
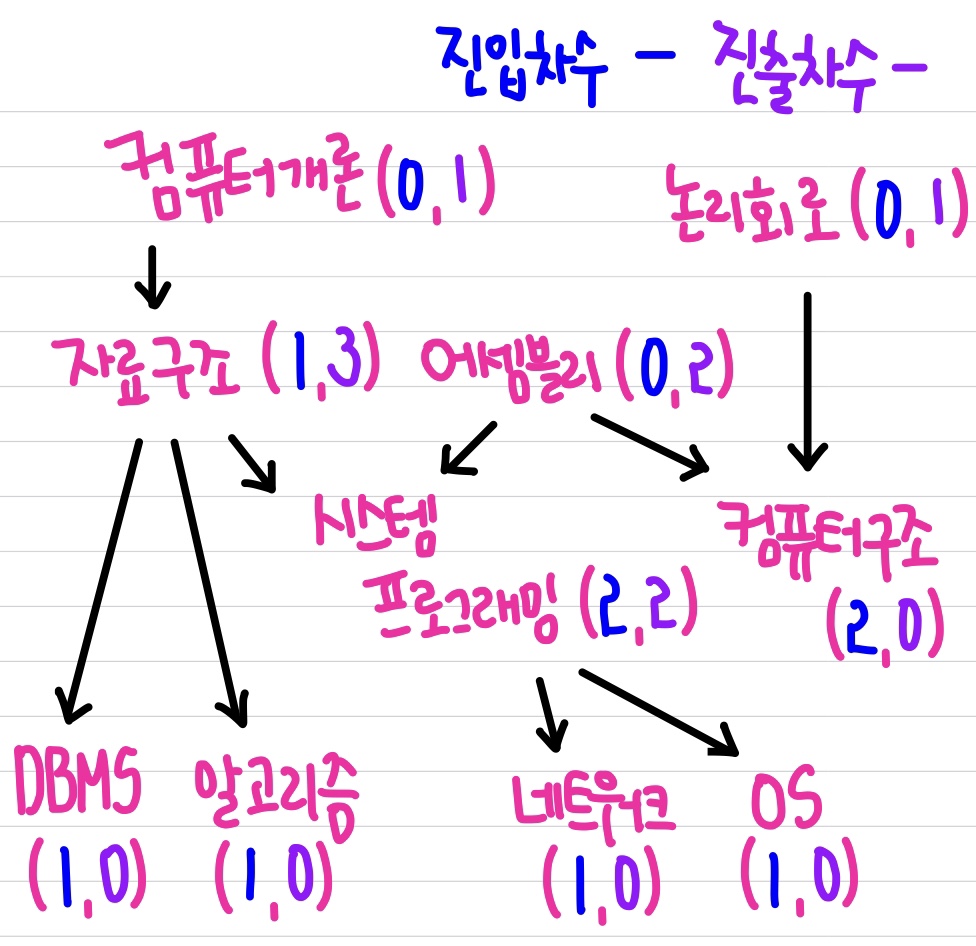
다음은 10 과목이 있다.
여기서 DBMS 를 들으려면 컴퓨터개론 -> 자료구조 -> DBMS 순으로 과목을 들어야한다.
다른 순서로는 학습을 할 수 없다.
이런 경우가 순서가 정해져있는 경우이며 순서들을 지키고 모든 정점을 나열하는 것이 위상 정렬이다.
그리고 진입차수와 진출차수의 개념을 알아야한다.
- 진입 차수 (Indegree) : 특정한 노드로 들어오는 간선의 개수
- 진출 차수 (Outdegree) : 특정한 노드로 나가는 간선의 개수 예시에 진입차수는 파란색, 진출차수는 보라색으로 각 정점마다 표현해두었다.
위상 정렬 특징
- 방향 그래프, 진입 차수, 진출 차수가 있다. ( 진입 차수가 중요하다. )
- 하나의 방향 그래프에는 여러 위상 정렬이 가능하다.
- 위상 정렬에서 가장 먼저 들어와야 하는 놈은 진입 차수가 0 인 정점이다.
- 위상 정렬 과정에서 그래프에 남아 있는 정점 중에 진입 차수가 0 인 정점이 없다면 위상 정렬 알고리즘은 중단 된다.
- 사이클이 있을 때는 위상 정렬을 할 수 없다 !
위상 정렬 과정
처음에 큐에 진입차수가 0 인 것을 다 삽입한다.
- 진입사수가 0인 정점과 이와 연결된 모든 간선을 지운다. ( 선행 처리 )
- 남아있는 정점의 진입차수를 갱신한다. ( 1씩 감소 )
- 그래프에 모든 정점이 없어질 때 까지 반복한다.
위상 정렬 예시
여러 문제들이 있다.
BOJ 2252 줄세우기
BOJ 2623 음악프로그램
BOJ 1948 임계경로
이 중에 줄 세우기 풀이를 적어보겠다.
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class main {
static int N; // 정점의 갯수
static int M; // 간선의 갯수
static ArrayList<Integer>[] list;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
M = sc.nextInt();
// 인접리스트
list = new ArrayList[N + 1];
for (int i = 0; i <= N; i++) {
list[i] = new ArrayList<Integer>();
}
// 위상정렬
// 1. 진입차수를 관리할 1차원 배열이 필요하다(정점의 개수만큼)
int[] inD = new int[N + 1]; // 초기값 0
// 입력
int x, y;
for (int i = 0; i < M; i++) {
x = sc.nextInt();
y = sc.nextInt();
list[x].add(y);
// 2. 입력받은면수 진입차수 배열에 진입차수를 누적한다.
inD[y]++;
}
// 3. 큐에 진입차수가 0인 것을 모두 삽입한다.
Queue<Integer> q = new LinkedList<Integer>();
for (int i = 1; i <= N; i++) {
if (inD[i] == 0) {
q.offer(i);
}
}
// 큐 사이즈가 0이면 위상정렬불가
if (q.size() == 0) {
return;
}
// 4. 큐사이즈가 빌때까지 자신과 연결된 정점의 진입차수를 1씩 감소한다.
// 감소된 진입차수가 0인 정점은 큐에 삽입한다.
ArrayList<Integer> res = new ArrayList<Integer>();
Integer cur = -1;
while (!q.isEmpty()) {
cur = q.poll();
// 자신의 할 일 구현
res.add(cur);
//자신과 연결된 정점의 진입차수를 1씩 감소한다.
for (int i = 0; i < list[cur].size(); i++) {
int idx = list[cur].get(i);
inD[idx]--;
//감소된 진입차수가 0인 정점은 큐에 삽입한다.
if (inD[idx] == 0) {
q.offer(idx);
}
}
}
//사이클 존재여부판단
if (res.size() != N) {
return;
}
for (int idx : res) {
System.out.print(idx + " ");
}
System.out.println();
}
}
👏 참조
https://velog.io/@kimdukbae/%EC%9C%84%EC%83%81-%EC%A0%95%EB%A0%AC-Topological-Sorting
