ALGORITHM_최소 신장 트리 ( MST )
📚 ALGORITHM

📚 최소 신장 트리 ( MST )
최소 신장 트리 ( MST ) 란?
최소 신장 트리 ( Minimum Spanning Tree ) 란
무향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리 이다.
여기서 신장 트리는
n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리이다.
MST는 정점과 간선의 개수가 많아지면 구하기 힘들다. 그래서 완탐으로 구하기보단 Greedy 알고리즘을 이용해서 구한다.
Greedy 알고리즘은 간단히 말해서 미래를 생각하지 않고 각 단계에서 가장 최선의 선택을 하는 기법이다.
MST를 풀이하는 알고리즘은 대표적으로 2가지가 있다.
크루스칼 알고리즘 ( KRUSKAL )
크루스칼 알고리즘은
간선을 하나씩 선택해서 MST 를 찾는 알고리즘이다.
- 최초, 모든 간선을 가중치에 따라 오름차순으로 정렬
- 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴
- 사이클이 존재하면 다음으로 가중치가 낮은 간선 선택
- n-1 간선이 선택될 때 까지 2를 반복
크루스칼 알고리즘은 간선 중심 그래프로 간선리스트를 만들어야 한다.
그래서 UNION-FIND 알고리즘을 이용해서 트리를 합치고, 부모 정점을 파악하고 사이클 여부를 파악해서 MST를 찾는다.
가장 중요한 것은 사이클을 파악하는 것이다. 사이클이 있으면 MST가 될 수 없다.
위의 모든 과정을 n-1 간선이 선택될 때까지 진행해서 MST를 찾아주면 된다.
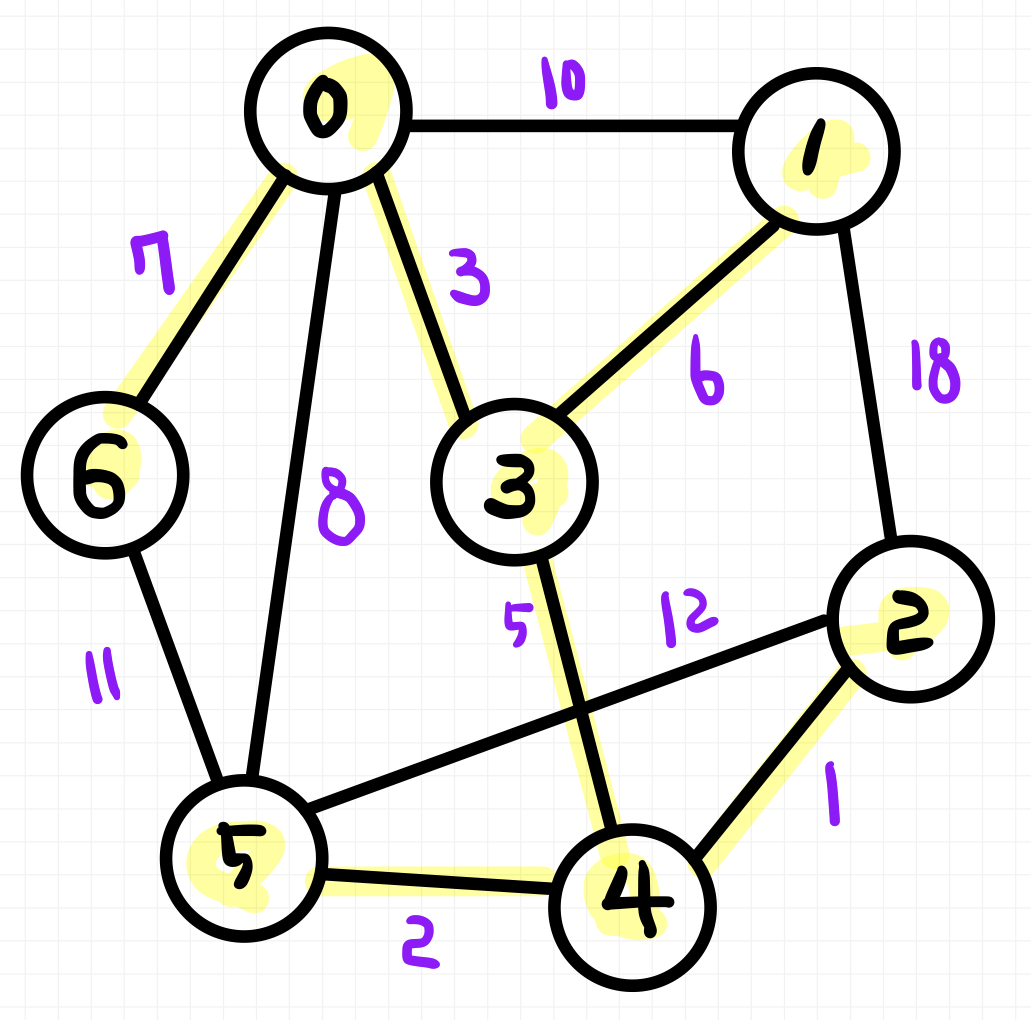
크루스칼 알고리즘 ( KRUSKAL ) 실습
- 문제
첫 번째 줄에 정점의 개수는 N개 간선의 개수는 V개로 입력을 받는다.
그 다음엔 V줄 만큼 from ( 출발 정점 ), to ( 도착 정점 ), weight ( 가중치 )가 순서대로 주어진다.
이 때 MST를 구하여라
- input
7 11
0 1 10
0 3 3
0 5 8
0 6 7
1 3 6
1 2 18
2 4 1
2 5 12
3 4 5
4 5 2
5 6 11
- output
24
- 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class MST {
public static class Edge implements Comparable<Edge>{
int from;
int to;
int weight;
public Edge(int from, int to, int weight){
this.from = from;
this.to = to;
this.weight = weight;
}
// 오름차순 정렬 ( 음의 가중치 포함 )
@Override
public int compareTo(Edge o) {
return o.weight >= this.weight ? -1:1;
}
}
// 정점의 개수
static int N;
// UNION-FIND Parents
static int[] parents;
// Edge List
static Edge[] edgeList;
// UNION-FIND START-----------------
// makeSet
// 새로운 집합 생성 - 초기 부모값을 다 본인을 가르키게 하기
static void makeSet(){
parents = new int[N];
for(int i=0; i<N; i++){
parents[i] = i;
}
}
// findSet
// a를 포함한 부모값 찾기
static int findSet(int a){
if(parents[a] == a) return a;
// Path Compression
// 노드의 부모 정보를 갱신 ( 쓸데없는 경로를 줄여줌 )
return parents[a] = findSet(parents[a]);
}
// union
// 트리 ( 집합 ) 를 합치기
static boolean union(int a, int b){
// a와 b의 부모값 찾기
int aRoot = findSet(a);
int bRoot = findSet(b);
// 만약 같으면 사이클이 생성되므로 실패
if(aRoot == bRoot) return false;
// 같지 않다면 같게 만들어 준다
// 부모값끼리 합쳐야한다.
parents[bRoot] = aRoot;
return true;
}
// UNION-FIND END-----------------
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st= new StringTokenizer(br.readLine()," ");
// 정점 개수 입력
N = Integer.parseInt(st.nextToken());
// 간선 개수 입력
int V = Integer.parseInt(st.nextToken());
// Edge 저장할 리스트 생성
edgeList = new Edge[V];
// 간선 개수 만큼 Edge 추가
for(int i=0; i<V; i++){
st = new StringTokenizer(br.readLine()," ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 리스크에 추가
edgeList[i] = new Edge(from,to,weight);
}
// 1. weight 로 오름차순 정렬해주기
Arrays.sort(edgeList);
// 새로운 집합 생성
makeSet();
// 결과 비용
int result = 0;
// 횟수 카운팅
int cnt = 0;
// 2. 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가
for(Edge edge : edgeList){
// edge.from 과 edge.to 를 같은 트리로 묶기
if(union(edge.from, edge.to)){
result += edge.weight;
// 3. N-1 간선이 선택되면 끝
if(++cnt == N-1){
break;
}
}
}
System.out.println(result);
}
}
- 가중치 오름차순 한 것
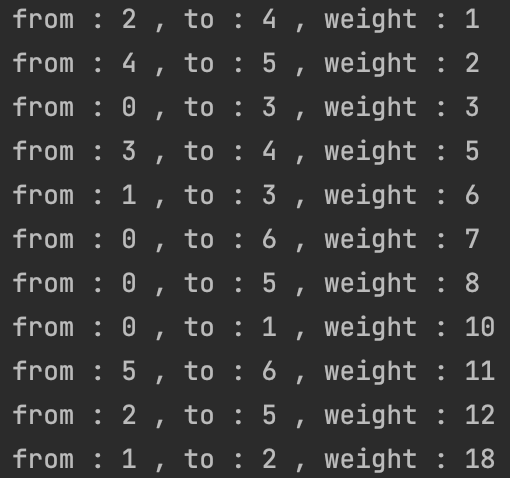
- MST Graph
위에 오름차순 순서대로 그래프에서 정점을 연결시켜주면 된다.
사이클이 생겼을 때는 연결해주지 않는 것이 중요하다 !!